A sphere derives its name from the Greek word “sphaira” which means “globe”. It is a geometrical object in 3d-space which is the ball’s surface. It is a 3d solid item consisting of a structure that is round in shape, similar to that of a circle. The area taken by the sphere is termed the surface area of the sphere. Alternatively, it can be defined as the area in total of the faces neighbouring it. The surface area of a sphere is generally expressed in terms of square units. The surface area of a sphere is given by A = 4πr2, where r represents the radius of the sphere.
Table of Contents
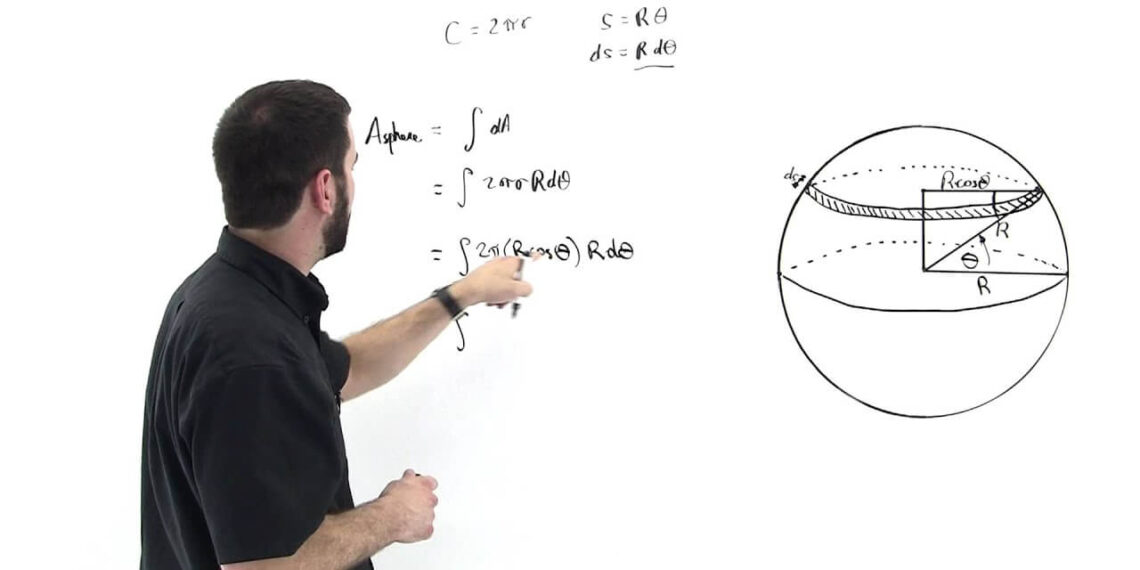
Surface Area of a Sphere – Formula Derivation
The derivation of the surface area of a sphere is given below.
It was discovered by Archimedes that if r is considered to be the radius of the sphere & cylinder, and with a height (h) that is the same as the length of the sphere’s diameter, then the sphere’s surface area is equivalent to the cylinder’s curved surface area. So, the relation between the surface area of a sphere and the curved surface area of a cylinder is:
The sphere’s surface area is the same as the curved surface area of the cylinder.
The sphere’s surface area = 2πrh
The height of cylinder (h) = diameter of sphere = 2 * radius = 2r
On putting h = 2r, we get
The sphere’s surface area is 2πrh = 2πr (2r) = 4πr2 square units.
The steps to compute the surface area of a sphere are as follows:
The sphere’s surface area is the scope of the sphere.
Step 1: From the question, determine the radius of the sphere.
Step 2: Multiply the radius of the sphere by itself to obtain the value of r2 (the radius square).
Step 3: Find the product of 4 and the value of r2.
Step 4: The above product obtained is multiplied by an approximate value of π, which is 3.14.
Step 5: The units are added to the final result.
Examples Based on Surface Area of a Sphere
Example 1: What is the surface area of a ball that is spherical with a radius of 9 inches?
Answer:
From the question, the radius of the sphere = 9 inches
r2 = 92 = 81in2
From the formula of the surface area of a sphere, A = 4πr2
On substituting the given values in the formula,
Surface area = 4πr2
= 4 × π × r2
= 4 × π × 81
= 1017.36
⇒ S = 1017.36 in2
∴ The surface area of the sphere is 1017.36 in2.
Example 2: A pilot is flying an air jet about the centre of the sphere whose radius is 20 feet, forming a circle. Find the surface area of the sphere. (Use π = 3.14).
Answer:
The radius of a sphere is given to be 20 feet.
r2 = 202 = 400 feet2
From the formula of the surface area of a sphere, A = 4πr2
On substituting the given values in the formula,
Surface area = 4πr2
= 4 * 3.14 * 400
= 5024 feet2
The surface area of the sphere is 5024 feet2.
The surface area of a sphere is discussed above, with the formula, notations, derivation of the formula along with a few solved examples. For more information on various mathematical concepts like the surface area of a cone, volume of a sphere, volume of a cube, volume of cuboid, definitions of total and lateral surface area, etc., please refer to BYJU’S website. It provides detailed explanations of these concepts, related formulae and solved problems.